Our aim is to find a way to prove recursive algorithms correct with means of automated first-order theorem proving. To do this, we were looking at the functional implementation of the QuickSort algorithm. That is, we want to prove sortedness and permutation equivalence for the output of such a computation. We already inspected of why this is in general hard and what kinds of mathematical “tools” we need to do this in some former blog posts. We will now put all of this together and shed light on how we succeed to prove this algorithm correct by means of superposition-based automated first-order theorem proving with Vampire. 

Essentially we require three steps

1. Specifying the algorithm with parameterized lists in first-order logic. 
2. Specifying the safety properties of sordidness and permutation equivalence in first-order logic. 
3. Apply superposition-based automated theorem proving with induction by manually splitting the proof into necessary lemmas so each inductive reasoning step can be performed by the automated prover. 

1. Specifying Divide-and-Conquer 

Many recursive sorting algorithms, as well as other recursive operations over lists, implement a divide-and-conquer approach: let f be a function following such a pattern, f uses (i) a partition function to divide list_a, that is a list of sort a, into two smaller sublists upon which f is recursively applied to, and (ii) calls a combination function that puts together the result of the recursive calls of f, e.g. append in our QuickSort algorithm in Figure 1. Figure 2 shows such a divide-and-conquer pattern, where the partition function partition uses an invertible operator ◦, with ◦^−1 being the complement of ◦; f is applied to the results of ◦ before these results are merged using the combination function combine. 

We formalize the first-order semantics of f via the function f : (list_a × ...) 7→ list_a, by translating the inductive function definitions of f to the following first-order formulas with parameterized lists (in first-order logic, function definitions can be considered as universally quantified equalities): 

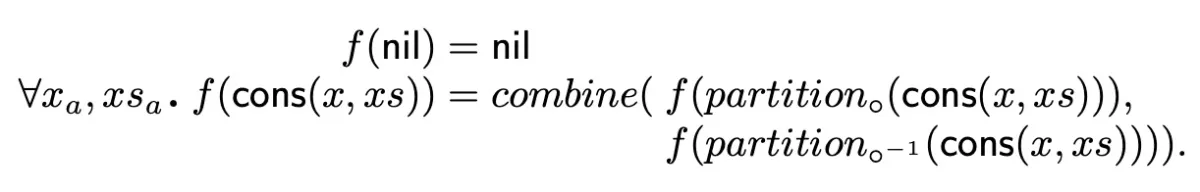
So to obtain the whole specification of the QuickSort algorithm, we apply this translation for every function: quicksort, append and filter (on each operation <, ≥). 

2. Specifying Sortedness and Permutation Equivalence

The functional behavior of quicksort in Figure 1 needs to satisfy two specifications implying the functional correctness of sort: (i) sortedness and (ii) permutations equivalence of the list computed by quicksort. 

(i) Sortedness: The list computed by the quicksort function must be sorted w.r.t. some linear order ≤ over the type of list elements. We define a parameterized version of this sortedness property using an inductive predicate sorted as follows 

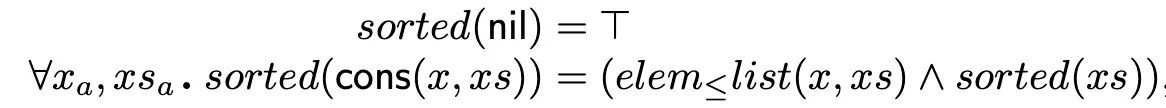
where elem≤list(x,xs) specifies that x ≤ y for any element y in xs. Proving the correctness of a sorting algorithm quicksort thus reduces to proving the validity of 

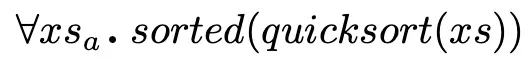
(ii) Permutation Equivalence: The list computed by the quicksort function is a permutation of the input list to the function. In other words the input and output lists of quicksort are permutations of each other, in short permutation equivalent. 

A common approach to prove permutation equivalence of two lists is to count the occurrence of elements in each list respectively and compare the occurrences of each element. Yet, counting adds a burden of arithmetic reasoning over naturals to the underlying prover, calling for additional applications of mathematical induction. We overcome these challenges of expressing permutation equivalence over equivalent sublists for any element of these lists. 

Analogously to counting the multiset multiplicity of x in ys via counting functions, we compare lists given by a filter= function, that similar to filter< returns all elements in the input list matching some element x as a list - avoiding the need to count the number of occurrences of x and hence prolific axiomatizations of arithmetic. Thus, to prove that the input/output lists of sort are permutation equivalent, we show that, for every list element x, the results of applying filter= to the input/output list of sort are the same over all elements. Formally we have 

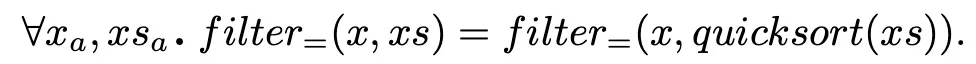
3. Proof Splitting to Establish Lemmas

To prove sortedness and permutation equivalence, we require a total of 7 and 2 lemmas respectively. However instead of just assuming these lemmas, they actually represent proof steps, where each lemma is automatically established by means of induction in the superposition-based theorem prover. These proofs are hence fully automated and don’t require us humans to reason about their correctness. 

Note this is “complementary” to how interactive theorem provers work: instead of specifying the necessary induction axiom ourselves, Vampire generates it during proof search. However, the proof of QuickSort is too complex for the prover to do all the steps at once. We thus had to formalize additional predicates to reason about smaller sublists etc. and split the proof apart accordingly. All of these proof splits represent lemmas that in contrast to most verification tools are established, that is their correctness is verified, by the prover itself, not by manually verifying the lemmas’ correctness. This is a major step towards fully automating the proof of QuickSort and more broadly proofs of recursive data structures with recursive function calls. 

We thus have a working proof of the sortedness and the permutation equivalence property of the QuickSort algorithm as displayed in Figure 1. For more technical details on induction, the used lemmas to prove QuickSort’s correctness and other sorting algorithms, see our preprint here.