My previous blog post (https://www.netidee.at/combining-shacl-and-ontologies/shacl-and-owl-part-3) mentioned a certain type of model: core universal models. This post is designed to provide some supporting information.

Domains and Relations

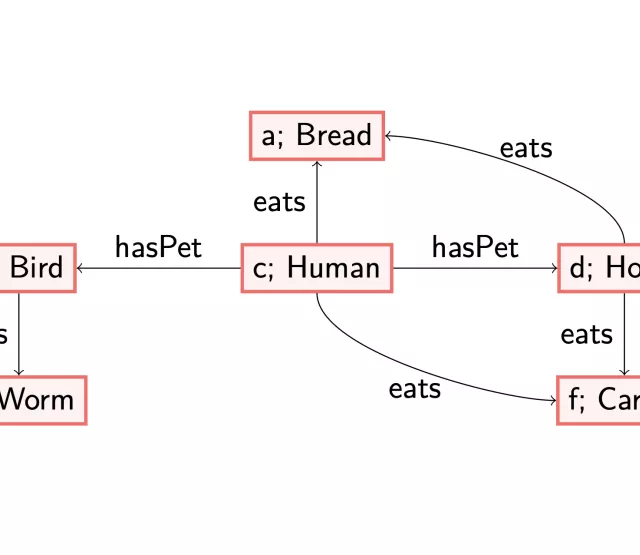
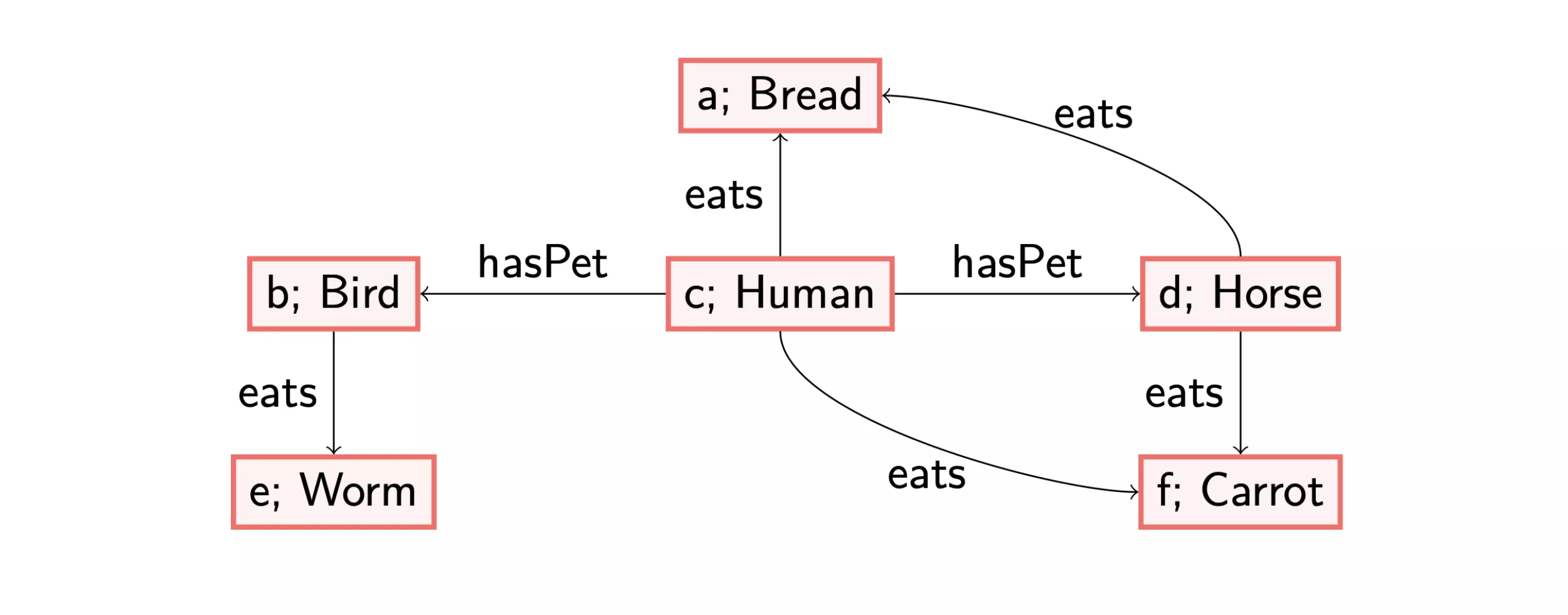
In logic, the words ‘model’ or ‘interpretation’ are used to denote a set of objects, the domain, and relations between those objects. An example of a domain are the people in a family, and the relations provided on this domain can be family relations, like ‘motherOf(a,b)’. In this case, we have two domain elements, that is, two people named ‘a’ and ‘b’. Furthermore, ‘is the mother of’ is a binary relation, as it ask for two inputs: the mother and the child. Relations can have any number of inputs: an example of a unary relation would be ‘Child(b)’: b is a child. Higher arities, the amount of inputs in a relation, are also possible, for instance ‘parentsOf(a,b,c)’, which can mean that a and b are the parents of c, or any other meaning we would like to give it in an interpretation.

In OWL, which is based on Description Logics (DLs), the arity of relations considered is limited: only unary and binary are allowed in the languages defined. That is, we focus on concepts, `Child(b)’ and roles ‘playsWith(b,c)’. Given some DL language, there are two types of information captured in a knowledge base: axioms and facts. All examples mentioned before are facts: they state some information that must be true for some objects a, b or c. Axioms may state things like: all children have someone to play with, or in DL syntax:

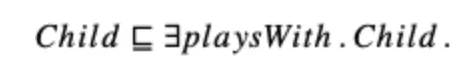
What can be expressed in such axioms, i.e., which operators are allowed, is dependent on which logic is chosen from the DL family.

What is a model?

Now suppose we are given such a knowledge base, consisting of axioms and facts. To decide whether a certain situation, a set of facts, is indeed modelled by this knowledge base, we first need to decide which objects are representing what in the fact set: maybe ‘b’ corresponds to some individual ‘Bo’ in the current situation. The next step is to check whether all facts in the knowledge base are represented in the considered situation: is there indeed a person named 'Bo', who is indeed considered to be a child? If the answer is no, the situation is not a model. Lastly, if the left-hand side of an axiom holds, we also need to check whether the right-hand side holds. That is, given that we assume Bo to be a child, there must exist a ‘playing with’ relationship with some other child. Now there are two options: either Bo is playing with Bo (playsWith(b,b)), or Bo is playing with some other child. In the first situation, we can confirm that the situation considered is indeed a model. In the second situation, there must exist some other child, suppose it is ‘Chris’, that Bo plays with. As Chris is a child too, the axiom is also concerning Chris: either Chris is playing with Chris, or with Bo, or with some other child. In the first two cases, we are done, in the third, we enter the loop again of having to consider another child in out model, etc. Note that we have to check this for every entity labelled with ‘Child’. To summarise, a certain fact set is a model if the facts contained in the knowledge base are ‘contained’ in the fact set, and moreover, there are no axioms only satisfied on the left-hand side.

When is a model 'universal’?

Instead of checking whether a given situation is a model, we can also talk about general structures that should appear to qualify as a model of a given knowledge base. That is, in the example discussed above, the general structure that must appear is the following.

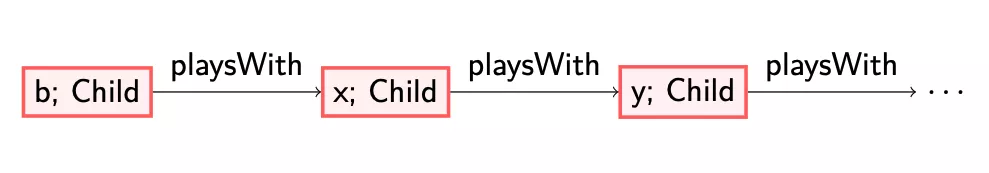
This structure is a universal model of the above defined knowledge base. To see that this is indeed a canonical structure, note that the case of Bo playing with Bo, corresponds to b is equal to x is equal to y, etc. The second case, Bo plays with Chris, who plays with Bo, is also captured by merging every even and every odd position in this canonical model: b is equal to y is equal to the node two further in the row, etc. and Chris corresponds to x, which is equal to the node following y, etc. Like this, the above structure can be embedded in each model. Mathematically speaking, we say that a model is universal if there exists a homomorphism from this specific model into any other model of the knowledge base.

Combining SHACL with OWL

So, why are we interested in models in this project? The basic question we are trying to answer is what it means to combine SHACL and OWL: i.e., when do we say that a certain knowledge base is validating a set of SHACL constraints with targets? SHACL constraints are looking for certain structures in a given fact set. A knowledge base provides both a fact set and a set of axioms, and has, in most cases, many fact sets that can function as their model. In other words, we are dealing with many fact sets instead of only one, which means that universal models are interesting to consider. As mentioned at the start of this blog, some more design choices of certain types of universal models are discussed in the previous blog post (https://www.netidee.at/combining-shacl-and-ontologies/shacl-and-owl-part-3).