Wer sind wir?

Manuel Leithner, Ludwig Kampel und Bernhard Garn sind Forscher in Informationssicherheit (MATRIS Research Group, SBA Research) und interessieren sich – unter anderem - für Stärken und Schwächen von künstlicher Intelligenz, inbesondere für Large Language Models (LLMs), welche die IT-Landschaft verändern und neue Kompetenzen von Benutzern verlangen.

Für wen ist KomMKonLLM?

Unsere Arbeit über die Konsistenz von Large Language Models hat als Zielgruppe nicht nur Wissenschaft und Forschung, sondern insbesondere auch Unternehmen, die LLMs in ihre Produktentwicklung oder Dienstleistungen integrieren (wollen) bzw. verwenden und sicherstellen wollen, dass ein gewisses Maß an Konsistenz – und in weiterer Hinsicht Akkuratheit – der Resultate gegeben ist.

Was bedeutet Konsistenztesten?

Das Konsistenztesten von LLMs adressiert das Problem, sicherzustellen, dass LLMs zuverlässig auf verschiedene Eingaben reagieren. Da LLMs oft komplexe und undurchsichtige Strukturen haben, können sie inkonsistente oder unerwartete Antworten auf ähnliche Eingaben geben. Diese Inkonsistenzen erschweren es, LLMs in Anwendungen einzusetzen, wo Verlässlichkeit entscheidend ist. Die Herausforderung liegt darin, geeignete Testmethoden zu entwickeln, die systematisch die Konsistenz der Modelle bewerten.

Herausforderungen:

Besonders beim Testen der semantischen Komplexität von LLMs ist es äußerst herausfordernd, die vielen möglichen Variationen von Formulierungen von Eingabeabfragen abzudecken. Wir werden daher automatisierte Methoden des kombinatorischen Testens verwenden, welche den Vorteil mit sich bringen, den modellierten Eingaberaum (in diesem Fall ein geschriebener Satz und die Arten diesen zu formulieren) bis zu einem gewissen vorgegebenen Grad - in einem bestimmten kombinatorischen Sinn - abzudecken. 

Wie funktioniert es?

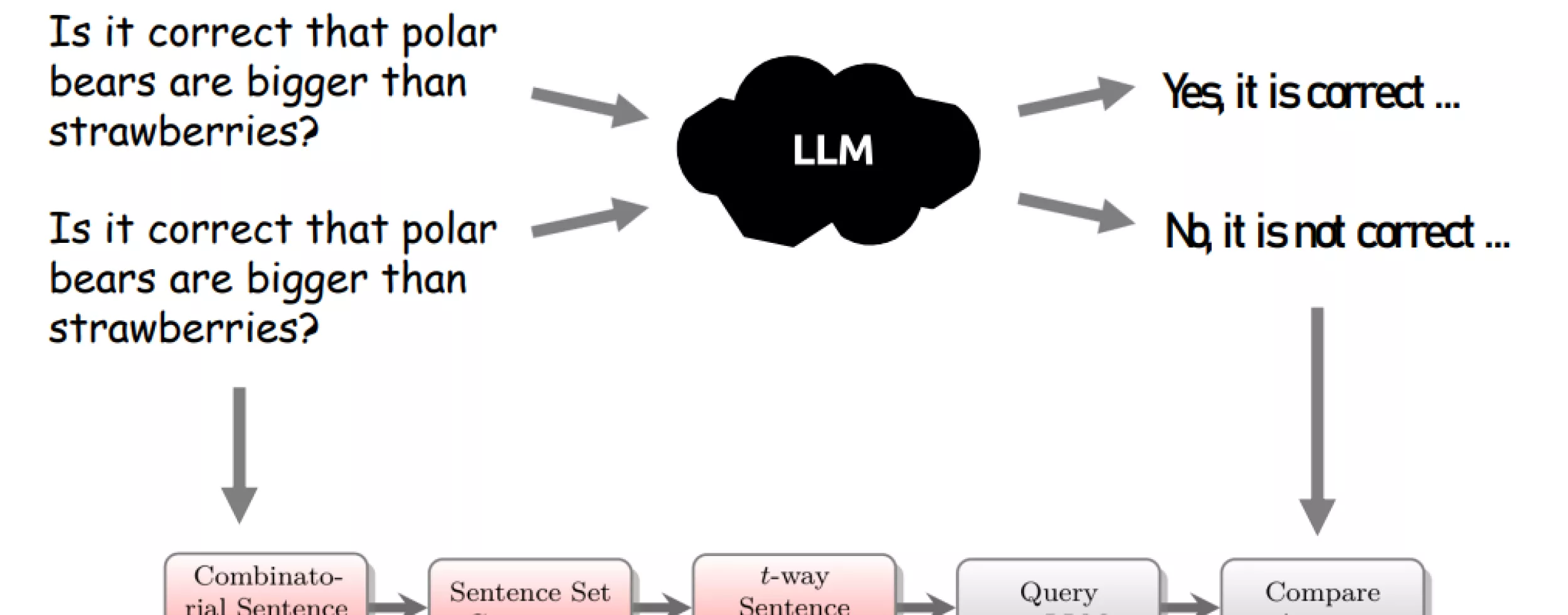
Wir wollen eine Serverlösung erstellen welche Konsistenztests für LLMs mit Hilfe von kombinatorischen Methoden automatisch erstellt, über offene Schnittstellen auf LLM-Instanzen ausführt und auch die Ergebnisse aufbereitet darstellen kann. Zusammen mit einem integrierten Repository von Testfällen bietet dies eine Lösung für das kombinatorische Testen der Konsistenz von LLMs.

Zusammengefasst schaut der gesamte Test-Prozess so aus:

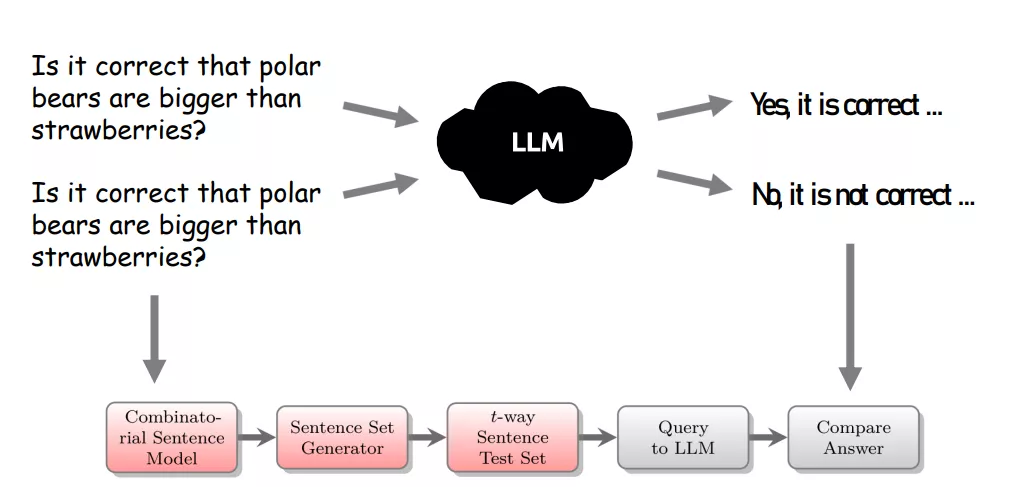
Besondere Bedeutung hat unser Projekt für:

• Internet-Technologie/-Infrastruktur
• Wirtschaftliche und/oder wissenschaftliche Kooperationen

Mehrwert für Internet-Technologie/-Infrastruktur:

Suchmaschinen und Chatbots sind integrale Teile der Internettechnologie und deren Interaktion mit Benutzern steht an zentraler Stelle. Die Integration von LLMs bietet neue Möglichkeiten zu intuitiveren Benutzerinteraktionen, dazu ist die Qualität der verwendeten LLMs sicherzustellen. 

Mehrwert wirtschaftliche/wissenschaftliche Kooperationen:

Wissenschaftliche Studien können mit Hilfe der entwickelten Serverlösung LLMs auf Konsistenz testen und auch bei Bedarf entsprechend weiterentwickeln. Die generierten Testdaten können in Benchmarks integriert werden. 

Projektergebnis:

• Eine Server-Software, welche Konsistenztests für LLMs mit Hilfe von kombinatorischen Methoden automatisch erstellt, über offene Schnittstellen auf LLM-Instanzen ausführt und auch die Ergebnisse aufbereitet darstellen kann. 
• Kombinatorisch generierte Testfälle zur Konsistenzevaluierung von LLMs in einem repository.