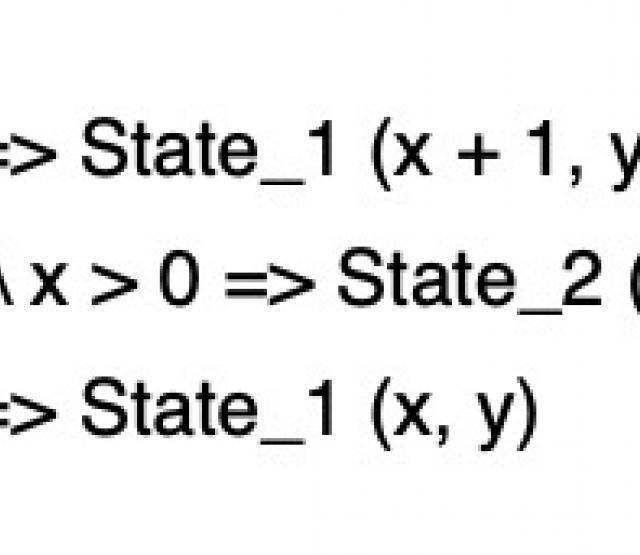Hallo allerseits,

Wie bereits in unserer Roadmap beschrieben, werden wir im Endeffekt einen sogenannten SMT-Solver nutzen um Smart Contracts zu analysieren. Zu diesem Zweck müssen wir die Semantik von Smart Contracts auf eine bestimmte Art und Weise enkodieren, so dass der SMT-Solver etwas mit ihr anfangen kann.

Ein SMT-Solver ist ein automatisiertes Lösungsprogramm für spezielle logische Probleme. In unserem Fall werden wir uns logische Probleme einer bestimmten Form anschauen. Um diese Form genauer beschreiben zu können, muss man zunächst ein paar Grundlagen der Logik kennen.

Die einfachste Form der Logik ist die so genannte Aussagenlogik. Die Idee ist, dass man Platzhalter (Variablen) für Aussagen, welche entweder wahr oder falsch sein können durch logische Konnektive verknüpft und so neue Aussagen erschafft. Angenommen, a steht für die Aussage “Wien ist eine schöne Stadt” und b steht für die Aussage “Viele Menschen lieben Wien”, dann kann man diese Aussagen mithilfe einer Konjunktion (⋀) zu einer neuen Aussage verbinden a ⋀ b, die besagt “Wien ist eine schöne Stadt und viele Menschen lieben Wien”. Ein weiteres logisches Konnektiv ist die Implikation (→), die intuitiv eine “wenn-dann”-Beziehung beschreibt. Die Aussage a → b meint “Falls Wien eine schöne Stadt ist, dann lieben viele Menschen Wien”. Insbesondere, bedeutet a → b, dass falls wir sicher wissen, dass a wahr ist (Wien also eine schöne Stadt ist), dann können auch mit Sicherheit schlussfolgern, dass b wahr ist (also viele Menschen Wien lieben). Sollte a aber falsch sein (Wien also keine schöne Stadt sein), bedeutet dies aber im Umkehrschluss nicht, dass b falsch sein muss (also nicht viele Menschen Wien trotzdem lieben). Vielmehr ist es so, dass wir aus dem Wahrheitswert von a nichts über den Wahrheitswert von Wien ableiten können.

Die Prädikatenlogik erweitert die Aussagenlogik nun um sogenannte Prädikate. Um genauer zu sein, werden Platzhalter, die für gesamte Aussagen stehen, durch kompliziertere Ausdrücke ersetzt, die eine Aussage genauer beschreiben. Ein Prädikat kann man sich als ein Objekt vorstellen, dass einer Entität eine Eigenschaft zuweist. Beispielsweise könnte man das Prädikat S(x) definieren, das meint “x ist eine schöne Stadt”, wobei x hier als Platzhalter für eine beliebige Stadt steht. Um “Wien ist eine schöne Stadt” auszudrücken, kann man nun einfach S(Wien) schreiben. Ähnlich könnte man nun ein Prädikat L(x) haben, welches ausdrückt “Viele Menschen lieben x”. Dann beschreiben wir “Viele Menschen lieben Wien” durch L(Wien). Entsprechend, könnten wir die Implikation von oben ausdrücken als S(Wien) → L(Wien). In der Prädikatenlogik kann man nun aber noch weitergehen: Angenommen, wir wollen nun nicht nur ausdrücken, dass wenn Wien eine schöne Stadt ist, viele Menschen Wien auch lieben, sondern wir wollen diesen Zusammenhang zwischen der Schönheit einer Stadt und der Liebe, die ihr zuteil wird, als eine Gesetzmäßigkeit für alle Städte ausdrücken. Dann können wir das in der Prädikat durch den Einsatz eines sogenannten Allquantors tun: ∀ x, S(x) → L(x) meint, dass für alle Dinge (Städte) x gilt: wenn x schön ist, dann lieben viele Menschen x.

Im Endeffekt sind es genau Aussagen dieser Form für die wir uns interessieren werden. Denn angenommen, wir wissen nun sicher, dass Wien eine schöne Stadt ist (also das S(Wien) wahr ist), und wir wissen, dass ∀ x, S(x) → L(x) gilt, dann können wir daraus schlussfolgern, dass auch L(Wien) gelten muss (also dass viele Menschen Wien lieben). Somit können wir aus einer wahren Aussage (S(Wien)) eine neue wahre Aussage (L(Wien)) herleiten.

Der SMT-Solver den wir verwenden, kann uns nun helfen herauszufinden, ob wir aus einer bestimmten Menge von anfänglichen Wahrheiten und einer Menge von Gesetzmäßigkeiten eine bestimmte Menge an neuen Wahrheiten ableiten können oder nicht.

Genauer gesagt, können wir beliebige Gesetzmäßigkeiten der Form ∀ x1 x2, P1(x1) ⋀ P2(x2)  …. → R(x1, x2, …) schreiben. Aussagen dieser Form werden auch als Horn Clauses bezeichnet (Randnotiz: wir haben das ganze hier ein bisschen vereinfacht: Prädikate können immer auch mehrere Variablen/Platzhalter haben und es gibt neben Prädikatanwendungen auch noch weitere Aussagen, die man schreiben kann, beispielsweise Gleichheiten).

Wie wir uns diese Fähigkeit des SMT-Solvers nun zunutze machen, um Smart Contracts zu analysieren, beschreiben wir in unserem nächsten Beitrag!

Bis zum nächsten Mal!

Euer EtherTrust Team