In meinem Blogeintrag zum Jahresende 2023 1 Jahr Netidee Förderung habe ich dieses Projekt bereits kurz erwähnt. Ich habe den englischen Namen "Compositionality" damals mit "Zerlegbarkeit" übersetzt. Heute möchte ich es lieber "Zusammensatzbarkeit" nennen. Für viele macht das wahrscheinlich einen eher geringen Unterschied. Ich finde allerdings das "Zerlegbarkeit" eine sehr wichtige Komponente vernachlässigt: Denn wir wollen unsere Spiele nicht nur zerlegen können, sondern vielmehr wollen wir sie mit anderen zusammensetzen können. Analog könnte man fast jedes gebastelte Haus zerlegen, viele wären danach aber zerstört und nicht wieder zu verwenden. Unter diesen Häusern, möchten wir das Legohaus sein, dessen Teile man anschließend wieder zusammenbauen kann.

Auffrischung CheckMate

Lasst uns kurz die Idee und die Funktionalität von CheckMate wiederholen (siehe auch CheckMate): CheckMate ist ein Tool zur Analyse der spieltheoretischen Sicherheit von Protokollen. Als User*in stellt man ein spieltheoretisches Modell des zu analysierenden Protokolls zur Verfügung und CheckMate teilt einem mit, ob das Protokoll (spieltheoretisch) sicher ist.

Ein Protokol nennen wir spieltheoretisch sicher, wenn es die folgenden zwei Eigenschaften erfüllt. In einem sicheren Protokoll kann einerseits Teilnehmenden, die den Regeln folgen, nichts "gestohlen" werden. Andererseits gibt es für keine Gruppe von Teilnehmenden eine Verhaltensweise die zu einem Ergebnis mit mehr Profit führt.

Neuerung für die nächste Generation

In der nächsten Generation von CheckMate wird diese allgemeine Funktionsweise, sowie die Definiton von spieltheoretischer Sicherheit beibehalten. Wie das Tool intern zu Schlussfolgerungen kommt, ändert sich allerdings weitgehend. Bisher hat CheckMate das gesamte spieltheoretische Modell auf einmal angeschaut, Formeln darüber aufgestellt und diese dann einem Automated Reasoning Tool übergeben (Details in "Steht der Bauer im Zimmer,.."). In Zukunft wird CheckMate das Modell in seine Einzelteile zerlegen, die Sicherheitsanalyse auf einem Teil des Modells durchführen und die Ergebnisse dann zusammensetzen, um das Endresultat zu bekommen.

Wir profitieren auf zwei Arten durch diese Änderung. Erstens wird die Laufzeit von der Analyse großer Protokolle verbessert. Ab einer gewissen Größe sind nämlich die durch CheckMate generierten Formeln so komplex, dass die im Hintergrund arbeitenden Automated Reasoners an ihre Grenzen stoßen. Durch das Aufteilen in mehrere Teilprobleme, bekommen die Automated Reasoners zwar mehrere, aber sehr viel einfachere Anfragen gestellt.

Zweitens ermöglicht diese Herangehensweise das Lego-artige Zusammenbauen von spieltheoretischen Modellen und deren Sicherheitseigenschaften. Das heißt, man könnte zum Beispiel ein Teilprotokoll modellieren und analysieren, und dann im gesamten Protokoll, anstelle des Teilprotokolls einfach nur die Sicherheitseigenschaften einfügen. Das Ergebnis der Sicherheitsanalyse durch CheckMate wäre trotzdem korrekt.

Wie kann das funktionieren?

Schauen wir uns ein einfaches Beispiel dazu an. Im linken Bild ist das spieltheoretische Modell des Markteinstiegs einer neuen Firma zu sehen. Es gibt 2 Parteien. Partei N, die neue Firma die darüber nachdenkt in einen neuen Markt einzusteigen, und Partei E, eine in diesem Markt bereits etablierte Firma. Die neue Firma N kann sich entscheiden in den neuen Markt einzusteigen, im Bild durch den Pfeil e dargestellt, oder nicht einzusteigen, durch den Pfeil n dargestellt. Sollte N in den Markt einsteigen, hat die andere Firma E ebenfalls eine Entscheidung zu treffen: Ignoriere ich die neue Konkurrentin N, dargestellt durch den Pfeil i, oder starte ich einen Preiskampf, Pfeil pk.

Je nachdem welche Aktionen gewählt wurden, ist das Ergebnis anders. Nach der Aktion n, macht Firma N zum Beispiel 0 Profit, während die Gewinne von Firma E unverändert nämlich p bleiben. In den untenstehenden Bildern, ist der erste Wert immer das Ergbnis für Firma N und der Zweite für Firma E.

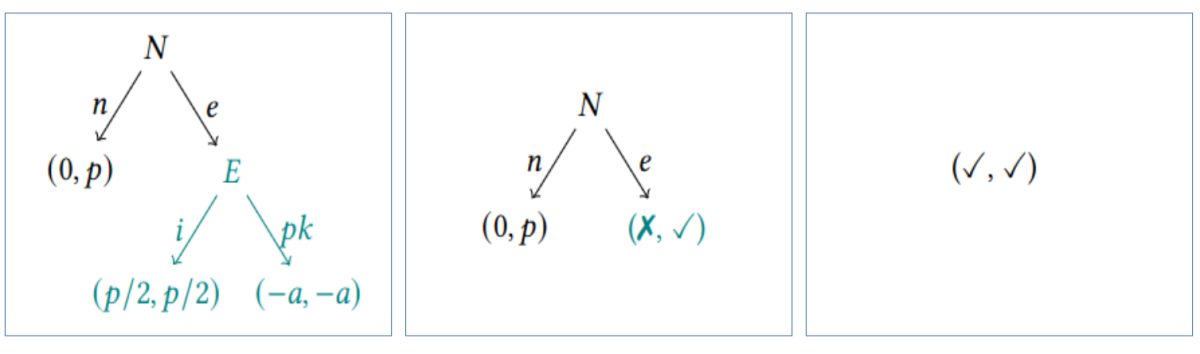
Wir fragen jetzt, ob dieses Modell eine unserer Sicherheitseigenschaften hat, nämlich, ob die Parteien Ergebnisse unter 0 vermeiden können. Wir nehmen dazu an, dass die Variablen a und p größer als 0 sind. Gemäß unserer neuen Herangehensweise betrachten wir zuerst den petrol eingefärbten Teil des Modells. Wir fragen uns: Kann die neue Firma N in diesem Teil so agieren, dass ihr Ergebnis größer als 0 ist? Die Antwort ist Nein, denn N kann in diesem Teil nichts entscheiden und -a ist kleiner als 0. Firma E kann in diesem Teil allerdings sehr wohl einen negativen Wert verhindern, daher ist die Eigenschaft für E erfüllt.

Dieses Zwischenergebnis (nicht erfüllt für N, erfüllt für E) fügen wir nun in das ganze Modell wieder ein, siehe mittleres Bild. Jetzt wiederholen wir den Vorgang und fragen: Kann N sich so verhalten, dass sie ein Ergebnis größer oder gleich 0 erhält? Diesesmal ist die Antwort Ja, denn N kann sich ja für den Pfeil n entscheiden. Auch für Firma E ist die Antwort Ja, obwohl E hier keine Entscheidung trifft. Egal wie sich N entscheidet E bekommt entweder p (> 0) oder wir kommen zu einem Teil der Modells, wo wir schon wissen, dass die Eigenschaft für E erfüllt ist.

Somit erreichen wir also das rechte Bild und können schlussfolgern, dass diese Eigenschaft in unserem kleinen Beispiel für alle Parteien erfüllt ist.

Wir haben in diesem Projekt in letzter Zeit tolle Fortschritte gemacht und sind nun dabei unsere theoretischen Erkenntnisse als CheckMates nächste Generation zu implementieren und hoffentlich auch bald zu veröffentlichen.