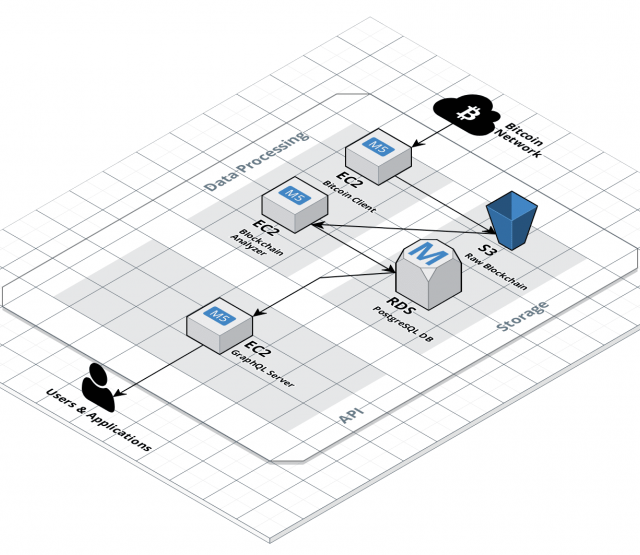
Als Teil unseres Projektes beschäftigen wir uns damit, wie man das Überweisungsverhalten von Teilnehmern in der Bitcoin Blockchain analysieren kann, um wiederkehrende Transaktions-Muster nachweisen zu können. Solche wiederkehrenden Strukturen weisen häufig auf automatisierte Überweisungs-Mechanismen hin, wie sie zum Beispiel von Malware angestoßen werden können. In diesem Beitrag möchten wir vorstellen, wie solche Muster mittels Graphentheorie erkannt werden können. Den Prototypen dieser Arbeit haben wir auf github veröffentlicht.

Die Bitcoin Blockchain bildet ein öffentliches Verzeichnis aller jemals durchgeführter Transaktionen. Diese Transaktions-Historie kann als Graph illustriert werden:

• die Knoten des Graphen  entsprechen den Adressen der Transaktions-Teilnehmer

• je zwei Knoten im Graphen sind durch eine Kante verbunden, wenn eine Transaktion zwischen den entsprechenden Adressen durchgeführt wurde

Da Transaktionen durch Kanten repräsentiert werden, können Teilgraphen als zeitlich lokale Transaktions-Abfolgen, oder Transaktions-”Muster”, verstanden werden. Diese Darstellung der Bitcoin Blockchain ermöglicht die Analyse von Transaktionen durch die Anwendung graphentheoretischer Algorithmen.

Das wiederkehrende Auftreten eines Transaktions-Musters in der Blockchain, entspricht damit dem wiederkehrenden Auftreten gleichartiger Teilgraphen in diesem Transaktionsgraph. Unser Prototyp bietet die Möglichkeit solche Teilgraphen auf Ähnlichkeit zu untersuchen, was erforderlich ist um deren Wiederauftreten nachweisen zu können. Dabei wird jedem Knoten eines Graphen ein Wert zugewiesen, der durch seinen Knotengrad bestimmt wird. Um festzustellen, ob zwei Teilgraphen eine ähnliche Struktur aufweisen, können die Werte der jeweiligen Knoten verglichen werden.

Hier eine Illustration eines simplen Graphen:

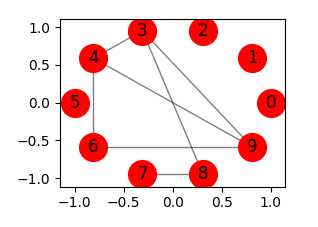
Den Knoten des Graphen werden durch unsere Software Werte zugewiesen, um sie anschließend Vergleichen zu können:

0 vs. 1 = 0.0

0 vs. 2 = 0.0

0 vs. 5 = 0.0

1 vs. 2 = 0.0

1 vs. 5 = 0.0

2 vs. 5 = 0.0

4 vs. 9 = 0.0

3 vs. 6 = 0.0044434564116

4 vs. 6 = 0.0044434564116

6 vs. 9 = 0.0044434564116

3 vs. 4 = 0.115852559292

3 vs. 9 = 0.132517373294

3 vs. 8 = 0.230183507595

4 vs. 8 = 0.230183507595

8 vs. 9 = 0.230183507595

6 vs. 8 = 0.364181448502

6 vs. 7 = 0.832449584601

7 vs. 8 = 0.832449584601

3 vs. 7 = 1.75819368327

4 vs. 7 = 3.26297247635

Diese Werte drücken eine Differenz aus. Betrachtet man die erste Zeile, werden die Knoten 0 und 1 als gleichwertig erkannt, was im illustrierten Graphen leicht erkennbar ist, denn beide Knoten besitzen keine Nachbarn. Dasselbe gilt auch für die Knoten 4 und 9, die jeweils mit drei weiteren Knoten verbunden sind.