SHACL and OWL are two popular standards for handling data on the semantic web; one is used to express constraints to check quality of the data (SHACL), the other for encoding implicit knowledge (OWL). Combining the two means being able to enforce certain structures on your data, while keeping the option open to encode for instance concept hierarchies.

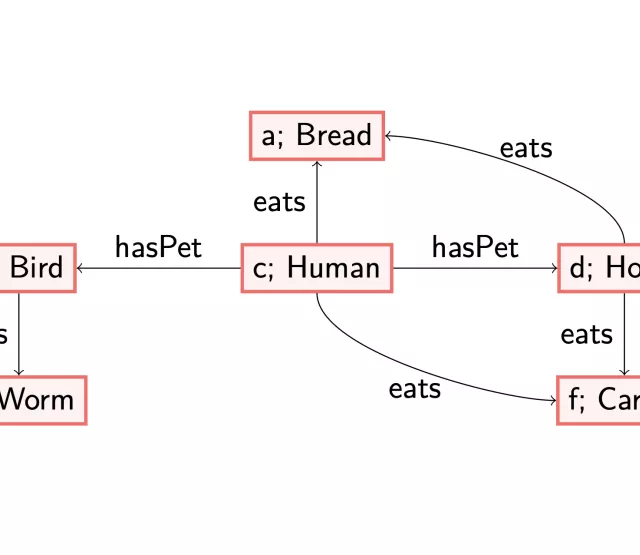
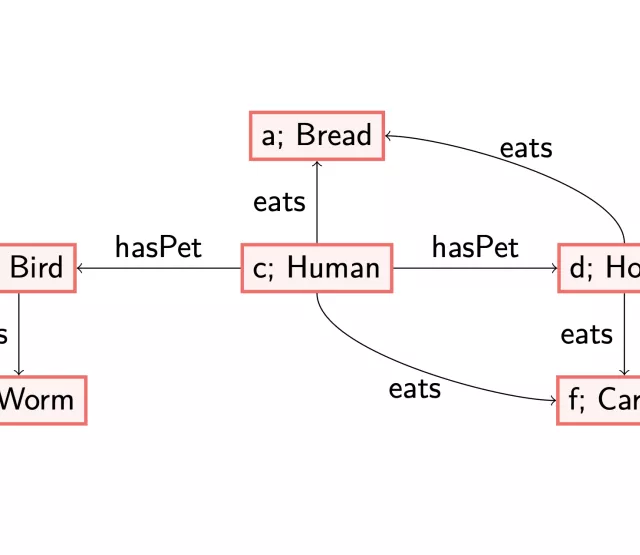
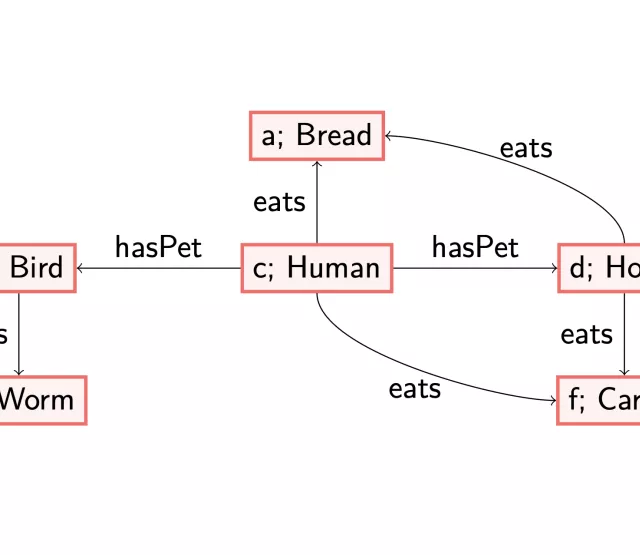
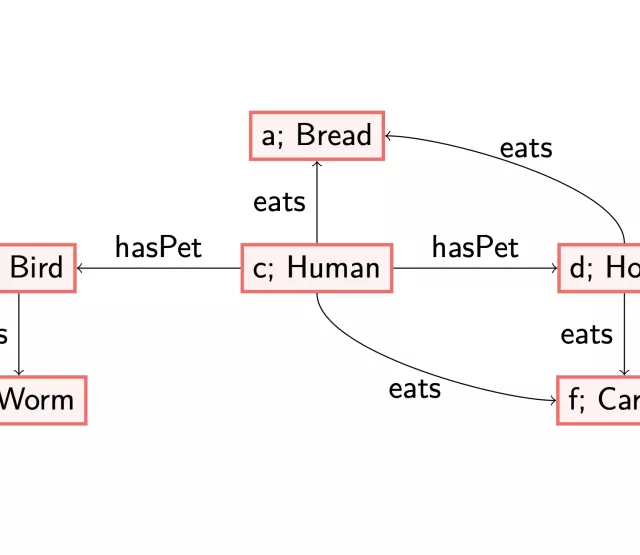
To make this more precise, we consider an example. We use the following data graph.

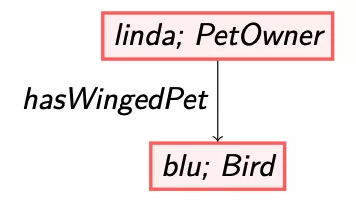
So, our data consists of linda, an individual with the label ‘PetOwner’, who owns a pet, blu. She has the relationship hasWingedPet, who is a ‘Bird’.

We use SHACL to validate this graph, that is, we have a (or more) constraint(s):

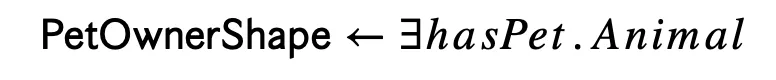
and a set of targets: PetOwnerShape(linda), i.e., we want to check whether we can find the PetOwnerShape-structure for linda. The required structure is an outgoing arrow labelled with hasPet. Moreover, the node reached by this arrow should contain the basic concept ‘Animal’. The graph above does not satisfy this requirement: there is no arrow with label hasPet leaving the node labelled with linda. Thus, in standard SHACL validation, this means that the above graph does not pass the test.

However, if we are allowed to reason using some reasoning rules, we see that the structure we have is close to the required structure. More precisely, if we would make precise that each ‘Bird’ must be an ‘Animal’ and that having a winged pet means having a pet,

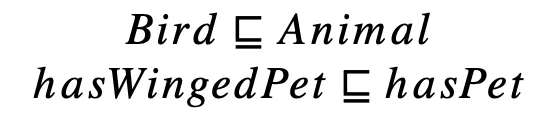
and we update the graph accordingly, we indeed find that the combination of the data graph and the axioms is enough to validate the shape graph.

Introducing new structures

In the above example we only considered relatively simple axioms and constraints for which it is straightforward what the combinations is supposed to mean: there is only one common sense way to materialise the implications of the axioms in the above data graph. That is, add that blue is an ‘Animal’, and add the relation hasPet to the arrow already decorated with hasWingedPet, and the validation result follows.

However, it is also possible to express the existence of whole structures in OWL: it may be stated that being a ‘Horse’ corresponds to having a hasParent outgoing arrow to a node labelled with ‘Horse’.

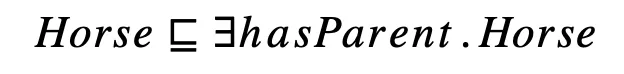
In that case there are different ways to materialise the implications of such an axiom: suppose we are given a ‘Horse’-labelled node, without an outgoing hasParent-edge. One of the possibilities to satisfy the described axiom is to add a hasParent-edge that starts and ends in this same node, meaning that this horse is its own parent, which would be weird in this example, but in general it is a possibility to be considered.

The other option is to add a fresh node that acts as the placeholder of the actual horse-parent of the ‘Horse’-labelled node. This means we do not declare which individual is the parent of the horse, but it allows us to reason about the existence of this horse. A drawback of the second method is that this freshly introduced blank node also has the label ‘Horse’ and no outgoing hasParent-edge either, as we did not introduce that yet, which means that we end up adding infinitely many blank nodes in a chain or eventually a horse that is its own parent.

To conclude, materialising facts is a promising and straightforward way to deal with the combination of SHACL and OWL as the example presented here shows. This seems to be an easy solution until you consider the more expressive features of SHACL and OWL. Knowing how to deal with the more complicated combinations of features is an open problem we try to solve in this research project.