We refer the reader to the first blog post in this series (https://www.netidee.at/combining-shacl-and-ontologies/shacl-and-owl) for more information on terms like SHACL, OWL, RDF, etc.

Repeated materialisation, also known as a chase procedure, is a way to build general models whose structure can be found in every model of the given data graph and ontology (mathematically: there exists a homomorphism). This makes the resulting structures suitable for many applications, for instance checking existence of certain substructures in all possible models. As SHACL is also a language that checks for existence of structures, this technique is very relevant for our case. However, we will see that the fact that SHACL also contains negation, i.e., checking for the absence of certain structures, means that we must refine our strategy.

Before we get to the actual technique, it is important to note that there can be roughly two types of axioms in ontology languages like OWL. First of all, axioms that have the power to create fresh structures, i.e., new nodes that are added to the data graph (the RDF data). We will refer to these axioms as existential axioms. And second, axioms that add new labels to existing structures. In the literature, the latter ones are called datalog axioms.

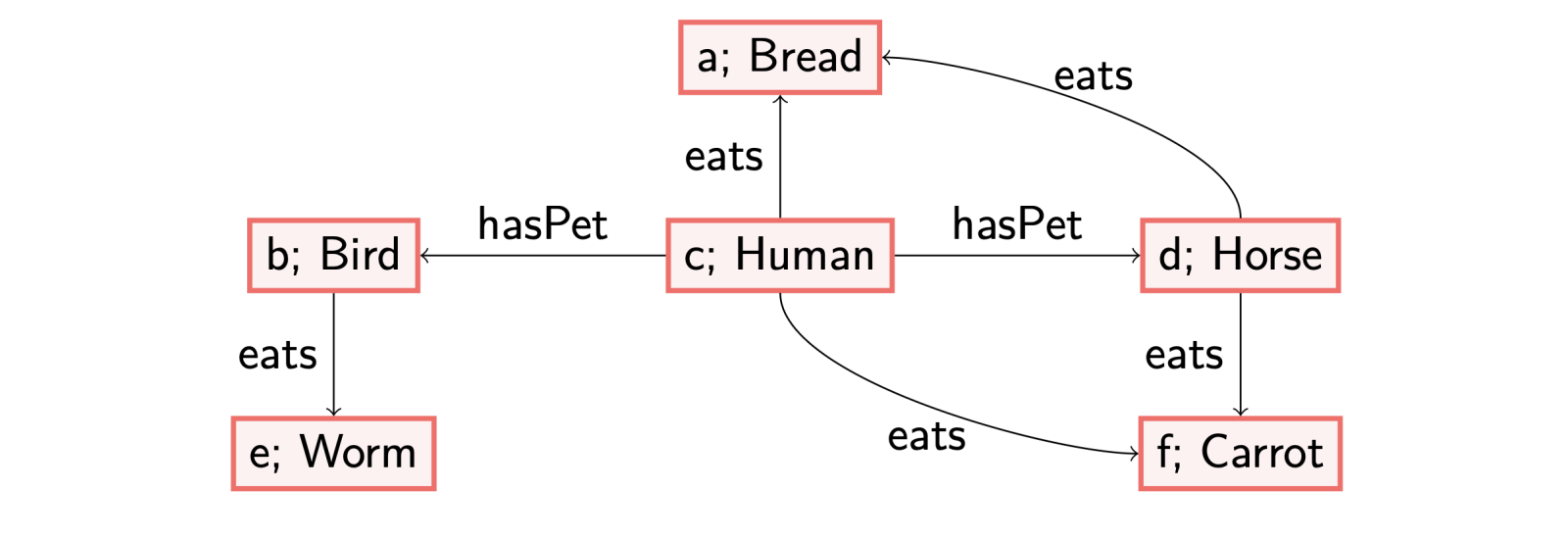
To illustrate this difference, let us consider two axioms: (1) each woman is a human, and (2) each country has an inhabitant that is human.

The first axiom is a datalog axiom, which labels all existing nodes with the label ‘Woman’ in the given data graph with the concept ‘Human’ too. The second axiom is an existential one: in case we encounter a node labelled with ‘Country’, there must be an outgoing edge labelled with ‘hasInhabitant’ to a node labelled with ‘Human’. A possible way to satisfy this axiom, called materialising, is to create a fresh/blank node, which serves as a placeholder of an individual, with the labels as described. This corresponds to knowing there exists a human, but without knowing their name. This allows us to reason about the existence of this Human. See also my previous blog post (https://www.netidee.at/combining-shacl-and-ontologies/shacl-and-owl-part-2) for another example and some more thoughts on this.

Consider for instance the following data graph.

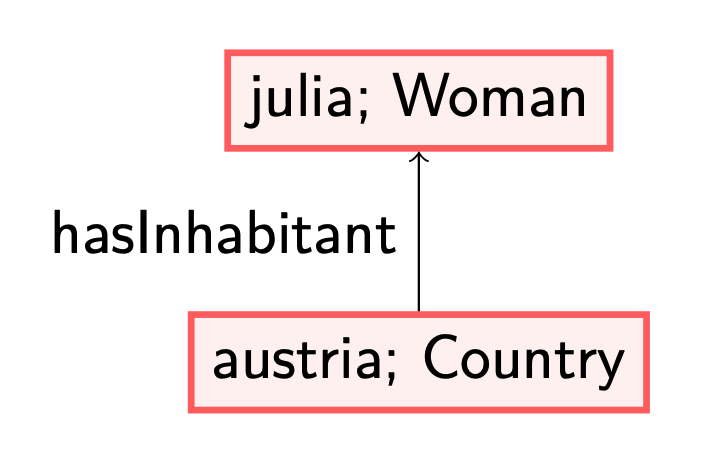
If we want this data graph to satisfy both (1) and (2), there are different orders in which we can add the information (i.e., materialise). These also result in different models. First applying rule (2) results in adding a blank node (in green, without a distinguished name, referred to with a variable ‘x’) as discussed before.

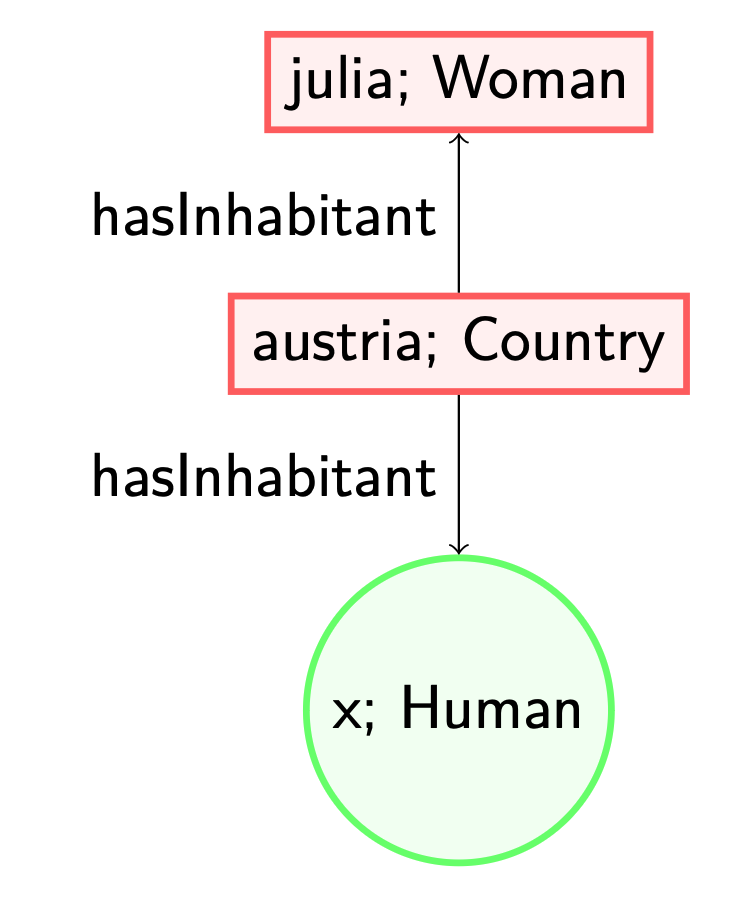
However, note that when we first would have applied (1), i.e., adding the label ‘Human’ to the node named after the individual ‘julia’, then adding a blank (green) node would not have been necessary to satisfy all axioms.

Note that when we are talking about materialising, we are not supposed to conclude solely on (2) that ‘julia’ must be a ‘Human’ - that would mean making new assumptions and thus breaking the generality (being a universal model in technical terms) of the structure we are building.

Next to changing the order in which axioms are materialised, you could also, for instance, ignore checking whether the right hand side of the axioms is already satisfied: creating the green node in any case, independent of whether ‘julia’ has the label ‘Human’ or not. Another approach is to add rules to the order in which rules can be applied, for instance, always giving priority to datalog axioms over existential ones. All these approaches produce a series of structures (chase procedure) such that the first one is the data graph, and every next structure is the result of materialising the right hand side of one axiom on the previous structure. The last structure in this series ideally satisfies all axioms. Ideally, as we might enter infinite loops in which the existence of something implies, possibly via multiple axioms, the existence of this same thing again (again, we refer the reader back to the example in the previous blog post). Different orders of applying the rules can have an effect on whether this procedure terminates or not.

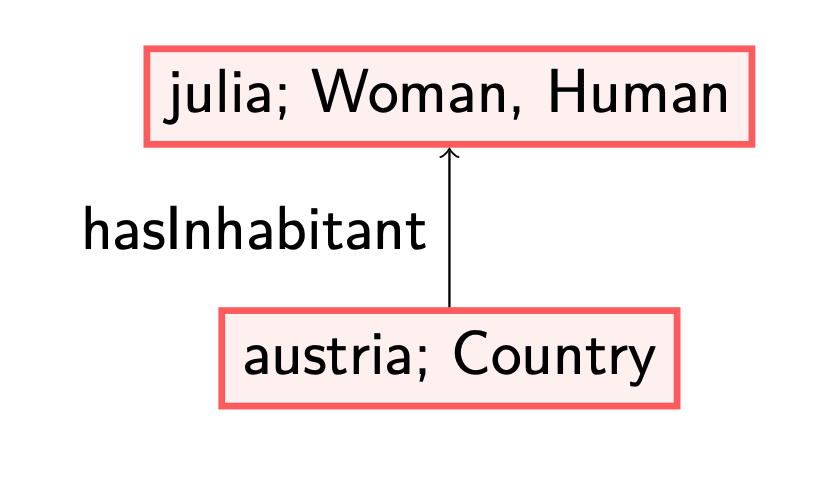
Both the last presented model, as the following, are structures that satisfy all axioms. Moreover, both are formed using a chase procedure.

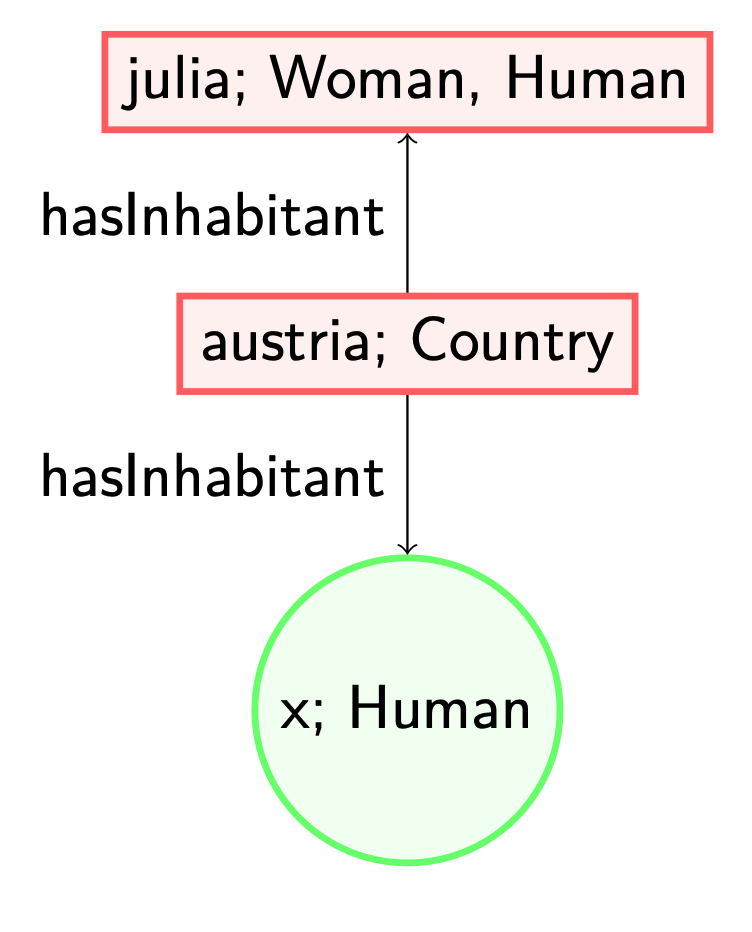
However, one of the two contains a redundant substructure. That is, a part of the structure can be mapped to another part of the structure: we can safely map ‘x’ to ‘julia’ such that no new labels are added to ‘julia’ or the ‘hasInhabitant’ relation between ‘austria’ and ‘julia’. The idea of being a core model is the lack of such redundant substructures. Only considering core models makes a difference when looking for the absence of certain structures: in SHACL, we can for instance check whether ‘austria’ is a country with an inhabitant that is not a woman. If we only know that ‘julia’ is an inhabitant of ‘austria’, it could be that she is the only inhabitant: we have no reason to assume otherwise with the given information.

In the literature, core models that are general (universal) are seen as the best way to reason about the possible absence of structures, as they make the least amount of assumptions. We follow this approach when defining SHACL validation in the presence of OWL: we define SHACL validation of a data graph in the presence of OWL as SHACL validation of this data graph with materisalised information in a core fashion derived from the OWL axioms.

The next step in our approach, which will be the topic of one of the next blog posts, is to get the same validation results by validating a new set of constraints, based on the ontology and the old set of constraints, against the same data graph we started with.