Das Konsistenztesten von LLMs adressiert das Problem, sicherzustellen, dass LLMs zuverlässig auf verschiedene Eingaben reagieren. In KomMKonLLM wenden wir kombinatorische Testmethoden aus dem Softwaretesten an, um Konsistenztests für LLMs zu generieren. Die in KomMKonLLM implementierte Methode zur Erzeugung von Konsistenztests für LLMs kann auf jede binäre Entscheidungsfrage (vereinfacht als Ja/Nein- bzw richtig/falsch-Frage beschreibbar) in natürlicher Sprache angewendet werden. Wir verwenden Wortersetzungen durch Synonyme und kombinatorische Methoden, um strukturiert und in (kombinatorisch-) messbarer Diversität abgewandelte Fragen zur Konsistenzevaluierung zu erstellen.

Ausgehend von einer gegebenen binären Entscheidungsfrage [1], gliedert sich der Gesamtprozess zur Erzeugung von kombinatorischen Konsistenztests in folgende Schritte:

In diesem Blog-Post beschreiben wir, was die ersten drei der obigen Schritte bewerkstelligen:

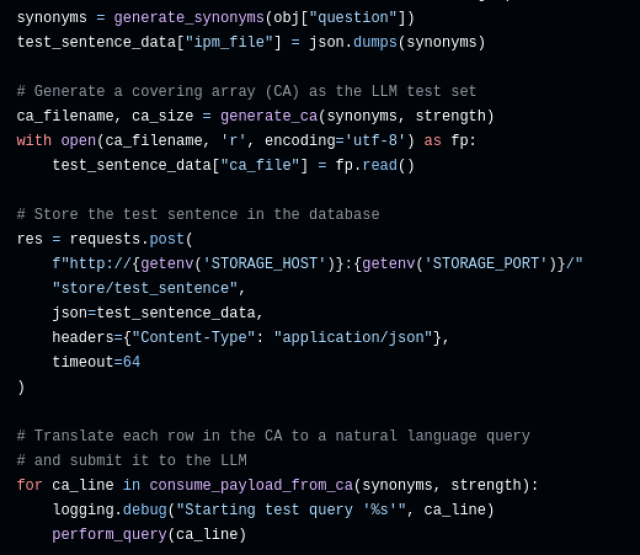
• „Linguistische Satzanalyse“: In diesem Schritt wenden wir NLP-Techniken an, um aus der gegebenen binären Entscheidungsfrage ein diskretisiertes Satzmodell zu erzeugen. Dazu spalten wir die Frage in ihre einzelnen Wörter auf und annotieren diese auch mit der entsprechenden lexikalischen Kategorie. Damit haben wir die Frage nun in endlich viele, in der gegebenen Reihenfolge angeordneten Elemente transformiert. Weiters wird eine Menge an lexikalischer Kategorien festgelegt, wo für entsprechende Worte Synonym-Ersetzungen anzuwenden sind. Zur weiteren Modellierung werden nun nur mehr Wörter dieser lexikalischen Klassen behandelt.
• „Kombinatorisches Satzmodell“: In diesem Schritt verwenden wir Synonym-Datenbanken, um für die in der Frage vorkommenden Wörter der ausgewählten lexikalischen Klassen eine bestimmte Anzahl an Synonymen auszuwählen, wobei  jedes Wort auch selbst als erstes Synonym in die entsprechende Liste hinzugefügt wird. Damit erhalten wir nun – im abstrakten Sinn - endlich viele Parameter (i.e., ausgewählte Wörter der Frage) zusammen mit ihren endlich vielen Parameter-Werten (i.e., selektierte Synonyme). Ein derartiges Modell wird im kombinatorischen Softwaretesten als IPM [2] bezeichnet.
• „Kombinatorische Frage-Erzeugung“: Basierend auf dem abgeleiteten IPM verwenden wir nun abdeckende Array-Strukturen (engl.: covering arrays), welche in minimalisierter Zeilenanzahl das Auftreten von allen t-fachen Parameter-Wertekombinationen garantieren. Geschickte Implementierungen fortschrittlicher Algorithmen ermöglichen es, diese Strukturen so zu erzeugen, dass eine große Reduktion in der Zeilenanzahl verglichen mit der Kardinalität des Kartesischen Produktes aller Parameter-Wertemengen erzielt wird [3]. Die garantierte t-fache Diversität innerhalb der erzeugten abdeckenden Array-Struktur bildet nun die Grundlage für eine strukturierte Konsistenzevaluierung eines LLMs. Die von uns verwendeten abdeckenden Arrays haben die Eigenschaft, dass in der ersten Zeile die ursprünglichen Worte selbst vorkommen.

Die letzten drei Schritte in obigem Prozess sind in einem weiteren Blog-Post beschrieben und wir widmen uns der examplarischen Durchführung des gesamten Prozesses in diesem nach-folgenden Blog-Post. 

[1] Man beachte, dass die Kenntnis der richtigen Antwort zu gegebener binärer Entscheidungsfrage für die Methodik von KomMKonLLM nicht notwendig ist.

[2] Die Abkürzung IPM steht für den englischen Ausdruck 'input parameter model', was man als ‚Eingabe-Parameter Modell‘ ins Deutsche übersetzen kann.

[3] Beispielsweise sei hier auf die Software CAgen verwiesen: https://srd.sba-research.org/tools/cagen/#/workspaces