Der erste Teil der Methodikbeschreibung von KomMKonLLM ist hier zu finden: Methodik von KomMKonLLM (Teil 1 von 2) | netidee

Um kurz zu wiederholen: Das Konsistenztesten von LLMs adressiert das Problem, sicherzustellen, dass LLMs zuverlässig auf verschiedene Eingaben reagieren. In KomMKonLLM wenden wir kombinatorische Testmethoden aus dem Softwaretesten an, um Konsistenztests für LLMs zu generieren. Ausgehend von einer gegebenen binären Entscheidungsfrage, gliedert sich der Gesamtprozess zur Erzeugung von kombinatorischen Konsistenztests in folgende Schritte:

Im vorherigen Blog-Post wurden die ersten drei Schritte in obigem Diagramm beschrieben, nun betrachten wir die letzten drei:

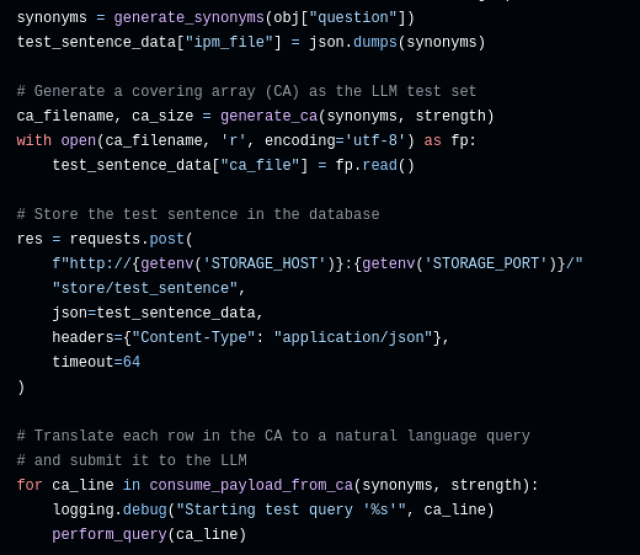
• „t-fache Konsistenzfragen“: Jede Zeile der im vorherigen Schritt erzeugten Array-Struktur kann nun wieder in eine Frage zurückgeführt werden, indem die Wörter durch ihre in der Zeile angegebenen Synonyme ersetzt werden. Dadurch erhält man nun kombinatorisch erzeugte abgewandelte Fragen, welche t-fache Diversität in der Synonymersetzung bieten.
• „Anfrage an LLM“: Jede der so erzeugten Fragen wird nun mit einem speziellen Prompt, der eine binäre Antwort des LLMs forcieren soll, an ein LLM gesendet und das Frage-Antwort Paar in einer Datenbank gespeichert. Aufgrund der Beschaffenheit der ersten Zeile der verwendeten abdeckenden Array-Struktur wird die ursprüngliche Frage als Erstes an das LLM gestellt.
• „Auswertung der Antworten“: Alle Frage/Resultat-Paare, welche basierend auf der abdeckenden Array-Struktur erstellt wurden, sind in der Datenbank verfügbar. Unter der Annahme, dass Synonymersetzungen die Semantik – und daher insbesondere auch die entsprechende (richtige) binäre Antwort – nicht verändern, ergibt sich die Konsistenzevaluierung nun aus dem Vergleich aller gespeicherten Resultat-Werte, welche – im besten Fall – alle gleich sein sollten. Sollte dies nicht der Fall sein, werden die abgewandelten Fragen mit abweichender Antwort aufbereitet dargestellt. Man beachte, dass dieser Vergleich für binäre Antworten im “Ja/Nein“-Format direkt implementierbar ist.

Der examplarischen Durchführung dieses Prozesses widmen wir uns in diesem folgenden Blog-Post. 

Anmerkungen zum obigen Prozess:

• Für jedes LLM muss ein Prompt gefunden werden, sodass nur binäre-Antworten zurückgegeben werden, sodass die direkte Vergleichbarkeit der Antworten zu verschiedenen (abgewandelten) Fragen sichergestellt ist.
• Der Parameter t, welcher die Diversität im Sinne der gleichzeitigen Synonymersetzungen in Fragen bestimmt, kann als Wertebereich innerhalb der natürlichen Zahlen Werte von eins [1] bis zur maximalen Anzahl an Worten mit entsprechender lexikalischer Kategorie annehmen. Je größer diese (Diversitäts-) Stärke [2] gewählt wird, desto mehr Zeilen haben die sich ergebenden abdeckenden Arrays. Jedoch erreicht man in der Praxis oft für nicht-maximale Stärke abdeckende Array-Strukturen, die immer noch signifikant weniger Zeilen haben als das entsprechende vollständige Kartesische Produkt der Parameter-Wertemenger aller Parameter des betrachteten IPMs.
• Für weitere Informationen zu kombinatorischem Software-Testen verweisen wir auf das "Automated Combinatorial Testing for Software"-Projekt des US NIST und für die in KomMKonLLM implementierte Methodik auf folgenden Konferenzbeitrag.

[1] Im Fall t = 1 sind die Synonymersetzungen für einzelne Worte unabhängig von einander. 

[2] In der englischen technischen Fachliteratur oftmals als strength bezeichnet.